长江日报融媒体3月14日讯 冬季来临,雪花漫天飞舞,好一个银装素裹的世界。人们把雪花放在显微镜下观察,会发现微小的雪晶呈现出既规律又复杂的结构。

雪晶的局部结构形态与整体结构形态高度相似。人们渐渐发现大自然中到处都有这种类似的结构,如:树枝的形状、河流的分支、海岸线等等,这些复杂而不规则的结构,在自然界中存在了几亿年,人们在感叹大自然鬼斧神工的同时,却始终没有触及到大自然中蕴含的科学真理,传统的欧式几何思考的是直线与圆,却没有合适的系统化的东西来记录真实世界的粗糙和不完美。比如:卵石,它是方的,还是圆的?对自然界这些不规则的、不光滑形状的描述,传统的欧式几何理论都是无能为力的,直到分形几何的创立才对这一自然现象进行了全新的奠基性的诠释。

自相似的树叶

自相似的花椰菜

拨开这层迷雾的人是谁?

他就是美籍法国数学家曼德尔布罗特。1967年曼德尔布罗特教授在总结测量英国海岸线时发现规律,在《科学》杂志上发表了文章《英国海岸线有多长?》,在当时以欧式几何理论为主导思想的学术界引起了巨大的轰动。

数学家曼德尔布罗特

英国的海岸线有多长难道不能测量出来吗?曼德尔布罗特说:任何海岸线,在某种意义上都是无限长的;在另种意义上说决定于你所选用的尺的长度。因为在不同尺度上描绘的海岸线图,都显示出相似的湾、岬分布。每一个大湾中都有小湾和小岬,那些小湾和小岬中又有更小的湾和岬;把这些湾和岬放大后和实际的海岸线仍然相似。正如曼德尔布罗特所说:“当你初次在一张比例尺为十万分之一的地图看到的一个海湾或半岛重新在一张比例尺为一万分之一的地图上被观察时,无数更小的海湾和更小的半岛就变得清晰可见了。在一张比例尺为一千分之一的地图上,更小更小的海湾和更小更小的半岛又出现了。”所以,你如果用一米的尺沿海岸测量,可以得出一个近似的长度,因为实际上你已经把小于一米的曲曲弯弯部分忽略掉了。如果改用一厘米的尺去量,一些小的曲折将被计入,得到的海岸线将会增长。随着测度标尺变小,海岸线的长度会不断加长,永远不会收敛于一个极限数值。其根本原因就在于海岸线是一个无穷嵌套的自相似结构。

他提出了“分形”一词,这是曼德尔布罗用拉丁词根进行拼造出来的,意思是细片、破碎、分数等等。接着,他给出了一个定义面较广的自相似分形概念:部分与整体以某种形式相似的形体称为分形。它描述的是相同的形状不断在越来越小的水平上复制。它们都有一个非常重要的性质就是反馈到自身,每一步的输出是下一步的输入。

武汉科技馆的数学展厅有一个叫做《美丽的分形》的展品,用一种直观的方式为大家展示了分形这种自反馈的特征。该展品在观众对面的屏幕处连接着摄像机,它同时拍摄着观众和大屏幕,这就在屏幕上形成了观众的多重循环影像。这是一个反馈回路的经典实例,一幅画在一幅画中,它们又在另一幅画中,细微的动作变化,对屏幕上成像产生影响。屏幕上的图像是观众自己生成的分形图形,有兴趣的观众不妨去试一试。

分形的另一个重要特点是尺度不变性。在一个分形图形中,无规则性或者支离破碎的程度,在任何尺度上都是相同的。即使你在放大镜下观测,这种无规则性或支离破碎的程度也不会减弱,它们仅仅是继续产生新的不规则性而已。

这种说法有何意义?科学家关于事物特征的描述最基本的莫过于问它有多大,持续多久。这都是依赖于标度(尺度)的一些基本性质。每种事物都有其特征尺度,例如天体物理学家描写的宇宙结构,大约在数百万光年的范围上;生物学家认识的微生物的结构大约有微米的长度;物理学家研究的夸克,约在10-13厘米的数量级上。每一个具体事物,都与特定的尺度相联系。几厘米长的昆虫与几米、十几米大小的巨兽在形态、结构上必然极不相同,否则它们就无法生存和繁衍。所以,尺度是十分重要的。试图对自然现象做定量描写时,就必须从特征尺度入手。

但是,分形几何学却否定了关于事物大小和久暂的区分的绝对尺度性,指出对于大自然的某些现象,去寻求特征尺度是毫无意义的。分形图形无法把微小的变化与宏大的变化分离开来,而是把它们紧紧地联系在一起。他所寻找的图像,无所谓小尺度和大尺度的差异,而是超越一切尺度;它不是左和右的对称、上和下的对称,而是大尺度与小尺度之间的对称,它是跨越尺度的对称性。

分形还有一个重要的数学性质,就是使用了分形维数。

首先,维数从何而来?

维数,又称维度,本意指数学中独立参数的数目。在物理学和哲学里,指独立的时空坐标的数目。

在传统的欧氏几何里,维数通常是整数。

•零维;

维数有什么用?

维数定义了我们感知这个世界的角度,拥有高纬度视角永远优于仅拥有低维度视角;

或者说,高维度包含了低维度的全部信息,低维是高维信息的投射。

维度和测量有着密切的关系。

例如:当我们画一根直线,如果我们用 0维的点来量它,其结果为无穷大,因为直线中包含无穷多个点;如果我们用一块平面来量它,其结果是 0,因为直线中不包含平面。那么,用怎样的尺度来测量它才会得到有限值?看来只有用与其同维数的小线段来测量它才会得到有限值,而这里直线的维数为 1。

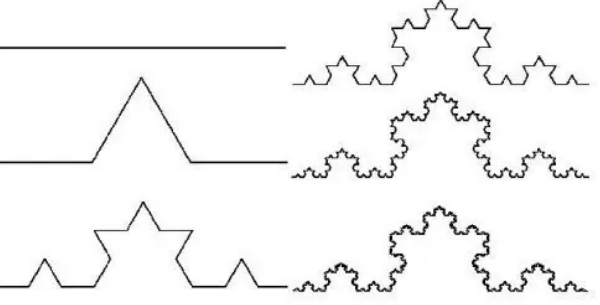
科赫分形曲线

分形图形却不能用整数维来测量,例如:科赫分形曲线其整体是一条无限长的线折叠而成,显然,用小直线段量,其结果是无穷大,而用平面量,其结果是 0(此曲线中不包含平面),那么只有找一个与科赫曲线维数相同的尺子量它才会得到有限值,而这个维数显然大于 1、小于 2,那么只能是小数了,所以存在分数维数。经过计算科赫曲线的维数是1.26。

这奇葩的1.26维是怎么算出来的呢?

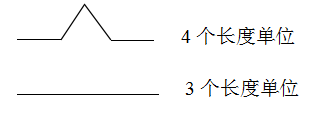
dim=log(4)/log(3)=1.26。

分形维数不同于传统的欧氏几何整数维,它更接近自然界的本质,自然界中多数事物无法用整数维进行描述,而分形维数能够很好的度量这些事物的空间维数,非整数维才是大自然的本质,整数维只是其中的特例。

如何用数学来描述分形这一自然性质呢?如果你能将其本质绘成图,那么图看起来是什么样的呢?你能够用一组简单的数学规则画出不像人工合成的图像吗?曼德尔布罗特给出了答案。他利用大量的电脑辅助,研究出一个曼德尔布罗特集,集合里的每个图形,都包含了无限多个更小的图形,子曼德尔布罗特集们会无限循环下去。但所有复杂图案都来源于一个简单的方程Z=Z*Z+C。

曼德尔布罗特集是这样的

分形理论在实际中的应用有哪些呢?

人们采用分形的方法,可以利用少量的数据生成各种不同的复杂图形,根据分形的自相似性,能够对图形图像进行有效的压缩。美国大片中电脑制作的逼真的植物、山川、云朵、人身上的细节都运用了分形原理。

影片中使用分形技术创造的场景

人们将分形几何和艺术结合在一起,创造了许多分形艺术画,它不同于普通的“电脑绘画”,而是利用分形几何原理,借助计算机强大的运算能力,将数学公式反复迭代运算,再结合作者的审美及艺术塑造,从而将抽象神秘的数学公式变成一幅幅精美绝伦的艺术画作。

下面是一些艺术家创作的分形艺术画。

分形几何为人们度量现实空间和地图上有许多类似海岸线那样的不规则曲线提供了数学工具;人们利用分形几何自相似性和空门填充性的特点,再结合天线的特征,使得分形几何在天线工程领域的应用有了突破性的进展。

分形理论在这些领域的成功尝试,极大地激发了科学研究工作者的兴趣,他们把分形理论逐渐扩展到其它的学科领域,如:哲学、数学、生物学、物理学、材料科学、医学、农学、气象学、天文学、计算机图形学、经济金融、历史研究、社会学、人类学等,可以说如今的分形无处不在。

(文中部分图片来自网络)

(武汉科技馆黄静)

【编辑:陈智】